Exponential Growth Formula Continuously Compounded Interest Formula
Formula to Calculate Exponential Growth
Exponential growth refers to the increase due to compounding of the data over time. It, therefore, follows a curve representing an exponential function.
Final value = Initial value * (1 + Annual Growth Rate/No of Compounding )No. of years * No. of compounding

You are free to use this image on your website, templates, etc, Please provide us with an attribution link Article Link to be Hyperlinked
For eg:
Source: Exponential Growth Formula (wallstreetmojo.com)
However, in the case of continuous compounding The continuous compounding formula depicts the interest received when constant compounding is done for an infinite number of periods. The four variables used for its computation are the principal amount, time, interest rate and the number of the compounding period. read more , the equation calculates the final value by multiplying the initial value and the exponential function, raised to the power of the annual growth rate into the number of years.
Mathematically, it represents as below,
Final value = Initial value * e Annual growth rate * No. of years.
Table of contents
- Formula to Calculate Exponential Growth
- Calculation of Exponential Growth (Step by Step)
- Example
- Monthly Compounding
- Quarterly Compounding
- Half Yearly Compounding
- Annual Compounding
- Continuous Compounding
- Calculator
- Relevance and Uses
- Recommended Articles
Calculation of Exponential Growth (Step by Step)
One can calculate the exponential growth using the following steps:
- Firstly, determine the initial value for which the final value one has to calculate. For instance, it can be the present value of money in the time value of money calculation.
- Next, determine the annual growth rate, which one can decide based on the type of application. For instance, if the formula is to calculate a future value formula of a deposit, then the growth rate will be the rate of return expected from the market situation.
- The tenure of the growth in terms of the number of years figured out, i.e., how long the value will be under such a steep growth trajectory.
- Now, determine the number of compounding periods per year. The compounding can be quarterly, half-yearly, annually, continuous, etc.
- Finally, the exponential growth is to calculate the final value by compounding the initial value (Step 1) by using an annual growth rate (Step 2), the number of years (Step 3), and the number compounding per year (Step 4), as shown above.
On the other hand, the formula for continuous compounding is to calculate the final value by multiplying the initial value (Step 1) and the exponential function raised to the power of the annual growth rate (Step 2) over several years (Step 3), as shown above.
Example
You can download this Exponential Growth Formula Excel Template here – Exponential Growth Formula Excel Template
Let us take the example of David. He deposited $50,000 in his bank account for three years at a 10% interest rate. Determine the value of the deposited money after three years if the compounding is:
- Monthly
- Quarterly
- Half Yearly
- Annually
- Continuously
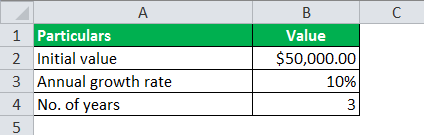
Monthly Compounding
No. of compounding per year = 12 (since monthly)
The calculation of exponential growth, i.e., the value of the deposited money after three years is done using the above formula,
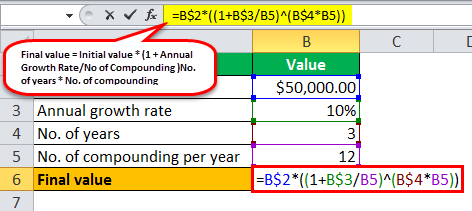
- Final value = $50,000 * (1 +10%/12 )3 * 12
The calculation will be-
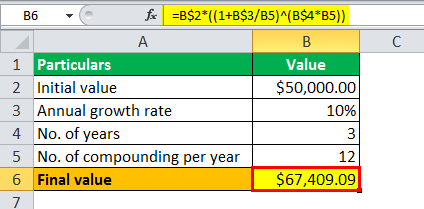
- Final value = $67,409.09
Quarterly Compounding
No. of compounding per year = 4 (since quarterly)
The calculation of exponential growth, i.e., the value of the deposited money after three years, is done using the above formula as,

Final value = $50,000 * (1 + 10%/4 )3 * 4
The calculation will be-
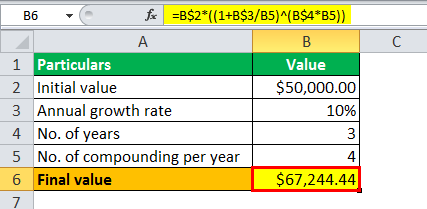
- Final value = $67,244.44
Half Yearly Compounding
No. of compounding per year = 2 (since half-yearly)
The value of the deposited money after three years done using the above formula:

Final value = $50,000 * (1 + 10%/2 )3 * 2
Calculation of Exponential Growth will be-
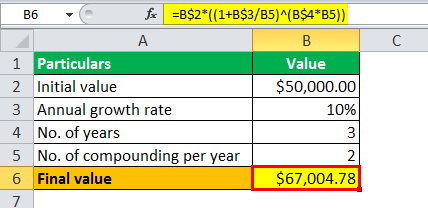
- Final value = $67,004.78
Annual Compounding
No. of compounding per year = 1 (since annual)
The calculation of exponential growth, i.e., the value of the deposited money after three years, is done using the above formula as,

Final value = $50,000 * (1 + 10%/1 )3 * 1
Calculation of Exponential Growth will be-
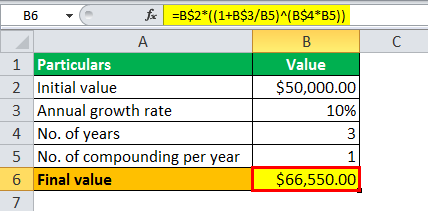
- Final value = $66,550.00
Continuous Compounding
Since continuous compounding, the value of the deposited money after three years money is calculated using the above formula as,
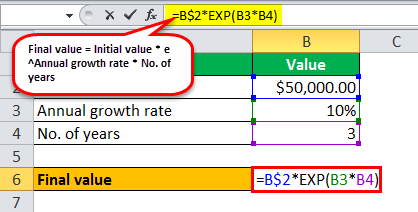
Final value = Initial value * e Annual growth rate * No. of years
Final value = $50,000 * e 10% * 3
Calculation of Exponential Growth will be-
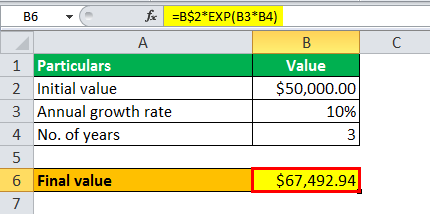
- Final value = $67,492.94
Calculator
You can use the following Exponential Growth Calculator.
| Initial Value | |
| Annual Growth Rate | |
| No. of Compounding | |
| No. of Years | |
| Exponential Growth Formula = | |
| Exponential Growth Formula = | Initial Value * (1 +Annual Growth Rate/No. of Compounding) No. of Years*No. of Compounding | |
| 0 * (1 +0/0) 0*0 = | 0 |
Relevance and Uses
A financial analyst needs to understand the exponential growth equation since it primarily calculates compound returns. The enormity of the concept in finance demonstrates the power of compounding to create a large sum with a significantly low initial capital. For the same reason, it holds great importance for investors who believe in long holding periods.
Recommended Articles
This article is a guide to the Exponential Growth Formula. Here, we discuss calculating exponential growth with examples and downloadable Excel sheets. You can learn more about financing from the following articles: –
- Exponential Distribution Exponential distribution refers to the continuous and constant probability distribution which is actually used to model the time period that a person needs to wait before the given event happens. This distribution is a continuous counterpart of a geometric distribution that is instead distinct. read more
- Growth Formula in Excel
- Calculate Sustainable Growth Rate
- Formula of Dividend Growth Rate
Source: https://www.wallstreetmojo.com/exponential-growth-formula/
0 Response to "Exponential Growth Formula Continuously Compounded Interest Formula"
Post a Comment